

The problem with the binary up-down counter with parallel load is that when it reaches the end of the count sequence, it always cycles back to zero. We can add a simple comparator circuit to this counter so that it will cycle back to this new input value rather than zero as shown in the next section. However, when the counter reaches the end of the count sequence, it will cycle back to zero and not to this new value. With this circuit, the count will start with whatever value is loaded into the register. In the first case, the counter is reset to zero immediately after the Clear is asserted while the latter case will reset the counter to zero at the next rising edge of the clock.
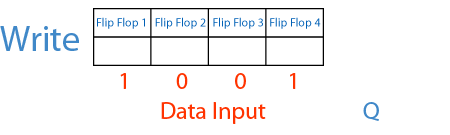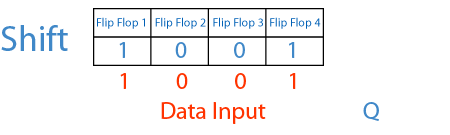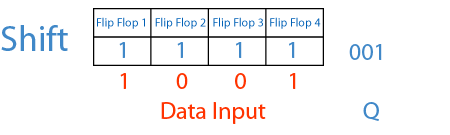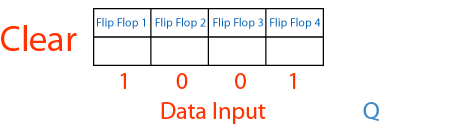
Notice that there is a timing difference between asserting the Clear line to reset the counter to zero as oppose to loading in a zero by asserting the Load line and setting the data input to a zero. We have kept the Clear line, so that the counter can still be initialized to zero at anytime. The operational table and logic symbol for this circuit is shown in Figure 20 (b) and (c). If the external input is selected, then whatever value is presented on the input data lines will be loaded into the register. If the HAS output is selected, then the circuit works exactly like before. By doing this, the input of the flip-flop can be selected from either an external input value if Load is asserted or the next count value from the HAS output if Load is de-asserted. The only difference between this circuit and that of Figure 17 (a) is that a 2-input multiplexer is added between the s output of the HAS and the D i input of the flip-flop. The modified counter circuit is shown in Figure 20 (a). With the value loaded into the register, we can now count starting from this new value. This is easily accomplished by modifying our counter circuit to allow it to load in an initial value. To make the binary counter more versatile, we need to be able to start the count sequence with any number rather than zero. Simulation trace for the 4-bit binary up-down counter.Ĩ.5.3 Binary Up-Down Counter with Parallel Load
#8 bit parallel in serial out shift register vhdl code code#
VHDL code for a 4-bit binary up-down counter. The two resulting equations areĬ out = D' a c in + D a' c in = (D a ) c in s = D' (a c in ) + D (a c in ) = a c inįigure 18. When we borrow, we get a 2, and 2 – 1 = 1, so s is also a 1. For example, for 0 – 1, we need to borrow, so c out is a 1. s is the difference of the subtraction and c out is a 1 if we need to borrow. For the bottom half, we are performing a subtraction of a The top half of the table is exactly the same as the HA truth table. Asserting D (setting to 1) will count down. The D signal is to select whether we want to count up or down.

The half adder/subtractor (HAS) truth table is shown in Figure 16 (a). We can design an n-bit binary up-down counter just like the up counter except that we need both an adder and a subtractor for the data input to the register.

Simulation trace for the 4-bit binary up counter. VARIABLE value: INTEGER RANGE 0 TO 15 BEGINĮLSIF (Clock'EVENT AND Clock='1') THEN IF Count = '1' THENįigure 14. The VHDL code for the 4-bit binary up counter is shown in Figure 14 and the simulation trace in Figure 15.ĪRCHITECTURE Behavioral OF counter IS BEGIN A 4-bit binary up counter with asynchronous clear: (a) circuit (b) truth table (c) logic symbol.


 0 kommentar(er)
0 kommentar(er)
